This subsubtopic explores how volumes of solids with triangular cross sections are determined by expressing cross-sectional dimensions from a base region and integrating accumulated triangular areas along a chosen axis.

Understanding Solids with Triangular Cross Sections

A solid with triangular cross sections is formed when a region in the plane (called the base region) is paired with a description of how a triangle is drawn perpendicular to an axis at every value of the input variable. The triangles change size smoothly depending on the width of the region at each point, producing a three-dimensional solid when accumulated.

A labeled pyramid illustrates how triangular faces define a three-dimensional geometric solid. This helps visualize how varying triangular slices can accumulate to form a full volume. The diagram contains only geometric labels and no extra calculus notation. Source.
When first discussing the base region, it is essential to recognize that this region determines the base length of each triangular slice. The base length refers to the horizontal or vertical dimension taken from the boundaries of the region and used to define the size of every cross-sectional triangle.

Because AP Calculus AB frames volume as accumulated area, triangular cross sections naturally extend the idea of integrating area formulas over an interval. Each triangular slice is treated as an infinitesimally thin region whose area contributes to the total volume.

Using Triangle Area Formulas in Volume Problems

To find the area of each triangular slice, students must select the correct triangle area formula depending on how the triangle is defined in the problem.

The most commonly used formula in this setting is the standard triangle area formula:

Students rely on this formula when the cross sections are described as right triangles, isosceles triangles, or equilateral triangles, each having a relationship between side lengths and height.

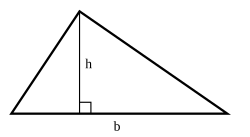
The labeled base and height clarify how the area formula $A=\tfrac12 bh$ is constructed. This parallels how triangular cross-sectional areas are defined before integrating to obtain volume. The diagram contains only essential geometric labeling. Source.
For example, if the problem specifies an equilateral triangle, its height can be written in terms of the side length using a geometric identity. If the triangle is a right triangle, the height may be equal to the given base or form a known ratio. AP problems may provide this relationship directly, or students may recall it from geometry.

Relating the Base Region to the Triangular Dimensions

The base region is typically bounded by curves or lines whose distance apart determines the dimension used in the triangle area formula. This dimension becomes the variable expression inserted into the area formula at each point along the axis of integration.

Students must determine whether the width of the region is more naturally expressed as a function of $x$ or of $y$. This choice dictates whether cross sections are taken perpendicular to the x-axis or y-axis. The selection does not change the underlying strategy but ensures the integral uses a consistent and correctly oriented variable.

A typical problem will specify that the triangular cross sections are perpendicular to an axis. This description indicates how each slice is positioned and clarifies which variable serves as the input for the area function.

The cross-sectional area depends entirely on how the base region’s boundaries determine the side length inserted into the triangle's area formula. Once this relationship is established, the volume comes from integrating this area across the interval that describes the solid's extent.

Setting Up the Volume Integral

Once the area of a triangle at position $x$ or $y$ is known, the total volume is found by integrating these areas over the appropriate interval. The definite integral represents the accumulation of all triangular slices.

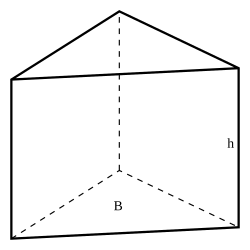
The triangular prism demonstrates volume as accumulated cross-sectional area, with constant triangular slices of area $B$ extended through height $h$. This supports the AP concept of volume as an accumulation of area. Only the geometric quantities $B$ and $h$ are displayed, with no additional notation. Source.

This expression emphasizes that the volume is built by summing infinitely many triangular cross sections whose areas vary with the input variable. Students interpret this integral as an accumulation of areas, consistent with the broader AP theme of viewing integrals as tools for combining infinitely many contributions of changing quantities.

Because triangular cross sections can take various forms in applied contexts, the formula for $A_{\triangle}(x)$ often changes depending on the type of triangle and how its dimensions relate to the base region. Regardless of the specific triangle, the fundamental strategy remains constant: express the triangular area in terms of the relevant variable, and integrate over the interval describing the solid.

Conceptual Interpretation in the AP Framework

This subsubtopic reinforces the broader AP Calculus AB principle that volume represents accumulated area, where geometric formulas interact with integration. Students learn to link geometric reasoning with calculus methods, translating a changing cross-sectional dimension into a function that becomes part of a definite integral. This synthesis of geometry and calculus highlights how three-dimensional quantities arise when two-dimensional shapes vary smoothly along an interval.